아스

* 해당 포스트는 <파이썬 알고리즘 인터뷰> 공부 후 정리 목적으로 작성되었습니다. *

leetcode 297번 ( https://leetcode.com/problems/serialize-and-deserialize-binary-tree/description/ )

✅교재를 참고하지 않은 풀이

📌BFS

(1) 직렬화

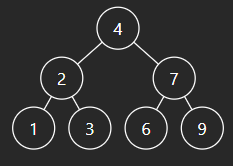
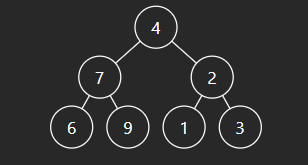
직렬화(TreeNode -> string) 로직에서는 root 노드 하나를 입력으로 받아서 그 아래 있는 노드들을 문자열 형식으로 출력해야 한다. 따라서 root 노드에서 시작해서 자식 노드들을 레벨 순서대로 순회해야 한다. 

1. 트리 전체의 노드를 데크에 레벨 순서대로 담기

이전 문제에서도 트리 전체를 탐색하는 데 BFS 방법을 사용한 것처럼, 큐(여기서는 데크)를 이용하면 트리의 모든 노드를 레벨 순서대로 순회할 수 있다. 파이썬의 데크 자료형은 리스트와 거의 유사하지만 내부적으로는 투 포인터를 사용해서 구현되었기 때문에 리스트의 맨 앞과 맨 뒤에서 원소를 추가하거나 삭제하는 데 O(1)이 소요된다. 

2. 불필요한 null 노드 제거하기

그러나 이대로 리스트로 변환할 수는 없고 추가 작업이 필요하다. 문제의 예시에서는 null인 노드가 있더라도 그 레벨보다 더 낮은 레벨에 노드가 존재하는 경우 'null' 값으로 표시되어야 하기 때문에 데크의 중간중간 null 값이 들어있다. 

위 그림의 경우 노드 값만 순서대로 나타내면 [1,2,3,4,5]이지만 중간의 빈 노드도 포함하기 때문에 실제로는 [1,2,3,null,null,4,5]가 리턴되어야 한다. 이렇게 나타내려면 left, right 자식 노드가 전부 null인 '2'번 노드를 탐색할 때도 2번 노드의 자식 노드를 큐에 추가해야 한다. 

그러나 이 방법대로 탐색하면 결과는 [1,2,3,null,null,4,5,null,null]로 출력된다. 4, 5번의 자식 노드가 없지만 2번과 같은 방법으로 탐색하여 null인 자식 노드가 큐에 추가되었기 때문이다. 

이를 수정하기 위해서 큐의 맨 뒤의 원소부터 탐색해서, null이 아닌 값이 나올 때까지 지우면 불필요한 null 노드(leaf 노드의 자식 노드)를 제거할 수 있다. 

3. 큐를 문자열로 변경

지금까지 작업했던 큐(데크) 형태의 자료형을 문자열로 바꿔서 출력해야 한다. str()로 큐를 문자열 형식으로 바꿔 준 다음, 출력 형식에 맞게 공백을 제거하고 "None"을 "null"로 바꾸는 추가 작업을 해서 바꿔준다. 

전체 직렬화 코드는 다음과 같다. 

def serialize(self, root):

    # use bfs
    if not root:
        return "[]"

    queue = collections.deque([root])
    array = []

    while queue:
        for _ in range(len(queue)):
            elem = queue.popleft()
            if elem is None:
                array.append(None)
            else:
                array.append(elem.val)
                queue.append(elem.left)
                queue.append(elem.right)

    while True:
        if array[-1] is None:
            array.pop()
        else:
            break

    result = str(array).replace(" ", "").replace("None", "null")
    return result

(2) 역직렬화

역직렬화(string->TreeNode) 로직에서는 앞서 문자열로 바꾼 값을 변환해서 트리의 모든 값을 left, right 자식 노드로 포함한 root 노드를 리턴해야 한다. 

1. 문자열을 리스트(배열)로 변환

앞서 추가 처리를 통해 데크를 문자열로 변환했었는데 이번에는 반대로 작업한다. 문자열의 앞뒤로 붙은 괄호[]를 제거한 뒤 ,로 구분된 원소들을 .split() 메소드를 사용해서 배열로 변환한다. 그러면 트리의 각 노드들의 값이 문자열 형태로 순서대로 저장된 배열을 얻을 수 있다. 

위의 트리 노드의 경우 ["1", "2", "3", "null", "null", "4", "5"]의 문자열 값들이 저장된 배열을 얻을 수 있다. 

2. 큐를 사용해서 배열의 값들을 추가로 트리 노드에 할당하기

위 배열의 값을 root 노드부터 순서대로(부모->자식 방향으로) 할당해야 한다. 앞서 레벨 순서대로 탐색하기 위해서 큐를 사용했는데, 같은 이유로 여기서도 큐를 사용한다. 

우선 root 노드의 값(1번 배열의 첫 번째 원소)을 가진 트리 노드를 선언한 뒤 해당 노드를 원소로 가진 큐를 선언한다. 트리 노드를 선언하는 데 사용된 배열의 값은 배열에서 제거해 준다. 

여기서의 배열은 큐가 아닌 리스트이지만 pop(0) 메소드를 사용하면 맨 앞에서도 원소를 제거할 수 있다. (물론 큐와 달리 O(1)이 아니라 O(n) 만큼의 시간이 걸린다.)

2-1. 배열의 값에 따라서 할당 방식을 다르게 하기

1번 배열의 맨 앞에서부터 값을 제거했을 때, 해당 값이 "null"일 수도, 문자열 형식의 숫자일 수도 있다. 

null 값이라면 트리 노드를 선언해서 값을 할당하지 않고 None 값을 할당하자.

반면 문자열 형식의 숫자(ex. "1")라면 해당 값을 숫자로 변환한 뒤 이 값을 value로 갖는 트리 노드를 선언해서 연결해 주자. 

이때 트리 노드는 위의 레벨에서 아래 레벨로, 왼쪽부터 오른쪽으로 할당되므로 한 노드의 자식 노드에 값을 할당할 때도 왼쪽 자식 노드부터 할당해 준다. 

전체 역직렬화 코드는 다음과 같다. 

def deserialize(self, data):

    if data == "[]":
        return None

    string = data.replace("[", "").replace("]", "")
    array = string.split(",")

    root = collections.deque([TreeNode(array.pop(0))])
    head = root[0]

    while root and array:
        elem = root.popleft()
        if elem is not None:
            if array:
                if array[0] == "null":
                    array.pop(0)
                    elem.left = None
                    root.append(None)
                else:
                    elem.left = TreeNode(int(array.pop(0)))
                    root.append(elem.left)
            if array:
                if array[0] == "null":
                    array.pop(0)
                    elem.right = None
                    root.append(None)
                else:
                    elem.right = TreeNode(int(array.pop(0)))
                    root.append(elem.right)

    return head

* 해당 포스트는 <파이썬 알고리즘 인터뷰> 공부 후 정리 목적으로 작성되었습니다. *

leetcode 617번 ( https://leetcode.com/problems/merge-two-binary-trees/ )

✅교재를 참고한 풀이

📌재귀

문제에서 주어진 기본함수를 재귀함수로 사용해서 문제를 푸는 방법이다. 

두 개의 트리를 합쳐야 하므로, 재귀함수에서는 두 트리 각각의 노드 하나씩을 입력으로 받는다. 

만약 두 트리 모두 노드가 있다면 두 노드값의 합을 값으로 가진 노드를 리턴한다. 

if root1 and root2:
    node = TreeNode(root1.val+root2.val)

노드를 리턴하기 전, 자식 노드들에 대해서도 새 값을 가진 TreeNode를 할당해 주어야 한다. 

왼쪽, 오른쪽 자식 노드에 대해서 각각 재귀함수를 호출해서 TreeNode를 계산해 준 다음에 값을 리턴한다. 

node.left = self.mergeTree(root1.left, root2.left)
node.right = self.mergeTree(root1.right, root2.right)

return node

두 트리 중 하나의 노드만 있다면 해당 노드를 리턴한다. 

해당 코드의 경우, 두 트리의 노드가 모두 없을 때에는 None을 리턴하게 된다.

else:
    return root1 or root2

💡post-order traversal(후위 순회)

코드가 실행되는 순서는 다음과 같다.

1. 현재 노드의 값(두 트리를 합쳤을 때 현재 노드의 위치에 오는 값) 계산

2. 현재 노드의 왼쪽 subtree들의 값 계산

3. 현재 노드의 오른쪽 subtree들의 값 계산

그러나 실제로는 2번과 3번(left subtree, right subtree의 값)이 계산된 후에야 parent 노드의 값이 계산되므로, 이 재귀함수는 postorder(후위 순회) 방식으로 탐색한다. 

후위 순회 방식에서는 다음 순서로 탐색한다. 

1. 노드의 left subtree

2. 노드의 right subtree

3. 노드 자신

* 해당 포스트는 <파이썬 알고리즘 인터뷰> 공부 후 정리 목적으로 작성되었습니다. *

leetcode 226번 ( https://leetcode.com/problems/invert-binary-tree/ )

✅교재를 참고하지 않은 풀이

📌DFS

이진 트리의 root 노드가 입력으로 주어질 때, 이진 트리를 좌우로 반전시키고 해당 트리의 root 노드를 리턴하는 문제이다. 

좌우로 반전시키려면 root 노드를 기준으로 왼쪽 subtree와 오른쪽 subtree를 바꾸면 된다. 

root 노드를 기준으로 모든 노드를 좌우 반전하려면 결국은 leaf 노드에서부터 작업을 시작해야 한다. 만약 leaf 노드까지 가지 않고 root 노드 바로 아래 레벨의 노드만 바꾼다면 아래 레벨의 노드들은 반전되지 않기 때문이다. 

예를 들어 다음과 같은 이진 트리를 입력받았다고 해 보자. 

만약 root 노드 바로 아래 레벨의 노드들 위치만 바꾸게 된다면 트리는 이런 모양이 된다. 

그러나 좌우 반전 트리는 모든 레벨의 노드들의 위치가 바뀌어야 하므로 위의 방법으로는 풀 수 없다. 좌우 반전은 아래처럼 7, 2 노드의 하위 노드들의 위치도 모두 바뀌어야 한다. 

따라서 재귀 함수를 사용해서 DFS 탐색으로 leaf 노드를 찾은 뒤, 해당 노드부터 다시 위 레벨로 올라오면서 자기 아래에 있는 두 노드의 위치를 바꾸는 방식으로 구현한다. 

또한 파이썬이 아닌 다른 언어(자바나 C언어)에서는 두 변수의 값을 바꿀 때 임시로 다른 변수 하나를 추가하는 방법을 쓴다. 

int a = 1;
int b = 2;

int temp = a;
a = b;
b = temp;

그러나 파이썬에서는 다중 할당을 사용할 수 있다. 

a = 1
b = 2

a, b = b, a

전체 코드는 다음과 같다. 

class Solution(object):

    def invertTree(self, root):
    
        def dfs(node):
            if not node:
                return
                
            dfs(node.left)
            dfs(node.right)
            
            if node.left and node.right:
                node.left, node.right = node.right, node.left
            elif node.left:
                node.left, node.right = None, node.left
            elif node.right:
                node.left, node.right = node.right, None
            
        head = root
        dfs(root)
        return head

✅교재를 참고한 풀이

📌재귀를 사용한 파이썬 방식

위의 DFS 방식을 그대로 사용하고 코드를 더 간소화할 수 있다. 중첩 함수를 사용하지 않고 주어진 함수를 그대로 호출해서 사용했다. 

if root:
    root.left, root.right = self.invertTree(root.right), self.invertTree(root.left)
    return root
return None

📌BFS

위에서는 leaf 노드부터 좌우 반전을 시작해야 한다고 적었지만 교재를 보니 BFS를 사용해서도 좌우 반전을 할 수 있었다. 

BFS의 경우 재귀함수로 구현이 불가능하므로 큐를 선언한 뒤 while문을 사용해서 큐의 앞에서 원소를 빼내고, 그 아래 레벨의 노드를 다시 큐의 맨 뒤에 넣으면서 구현했다. 

DFS는 leaf 노드부터 탐색이 진행되지만 BFS에서는 root 노드부터 시작해서 아래로 내려가면서 노드를 바꾼다. 

전체 코드는 다음과 같다. 

class Solution(object):

    def invertTree(self, root):
        queue = collections.deque([root])

        while queue:
            current = queue.popleft()
            if current:
                current.left, current.right = current.right, current.left
                queue.append(current.left)
                queue.append(current.right)

        return root

📌DFS

위의 코드에서 한 줄만 바꾸면 BFS 대신 DFS로 구현할 수 있다고 한다. 

BFS는 FIFO인 큐를 사용하는 반면 DFS는 LIFO인 스택을 사용하므로, 큐의 맨 앞에서부터 노드를 빼내던 로직을 큐의 맨 뒤에서부터 노드를 제거하도록 수정하면 된다. 

참고한 포스트

https://velog.io/@hysong/%ED%8C%8C%EC%9D%B4%EC%8D%AC-%EB%8B%A4%EC%A4%91-%ED%95%A0%EB%8B%B9Multiple-Assignment

* 해당 포스트는 <파이썬 알고리즘 인터뷰> 공부 후 정리 목적으로 작성되었습니다. *

leetcode 687번 ( https://leetcode.com/problems/longest-univalue-path/ )

✅교재를 참고하지 않고 시도: DFS -> 실패

한 노드에 대해서 2개의 자식 노드가 있을 때, 해당 노드와 자식 노드의 값이 같을 때 DFS 탐색을 하고 값을 1씩 증가시키는 로직을 구현했다. 

그러나 위 그림처럼 여러 개의 값이 연속되는 트리가 입력으로 주어지면 중간에 다른 값이 나올 때는 DFS 탐색이 되지 않게 되어 오류가 발생한다. 

따라서 값이 연속되건 되지 않건 모든 경우에 DFS 탐색이 되어야 하고, 다만 노드와 자식 노드의 값이 같은지 다른지에 따라서 DFS 탐색을 한 값을 그대로 사용하거나 바꾸도록 구현해야 하겠다. 

class Solution(object):
    longest = 0

    def longestUnivaluePath(self, root):
        
        def dfs(node):

            if not node or (not node.left and not node.right):
                return 0

            left, right = 0, 0
            if node.left and node.val == node.left.val:
                left = dfs(node.left)
            if node.right and node.val == node.right.val:
                right = dfs(node.right)

            if left != 0 and right != 0:
                self.longest = max(self.longest, left + right + 2)
            elif left != 0:
                self.longest = max(self.longest, left)
            elif right != 0:
                self.longest = max(self.longest, right)
                
            return max(left, right) + 1

        result = dfs(root)
        return self.longest

✅교재를 참고해서 시도: DFS 

1. 클래스 변수 사용

교재에서도 DFS를 사용해서 진행하였다. 이전 문제와 같은 이유로 클래스 변수를 선언하고 가장 긴 동일값의 경로는 해당 변수에 저장하는 방법을 사용했다.

중첩 함수 내부에서 지역 변수를 사용하지 않은 이유는, '가장 긴 동일값의 경로'는 정수 형식이라서 불변 객체(immutable object)이고, 불변 객체인 변수는 중첩 함수의 내부에서 같은 이름으로 사용되더라도 값이 변경되지 않기 때문이다. 즉 중첩 함수 내부에서 값을 바꿔도 중첩 함수 바깥의 로컬 변수의 값이 변경되지 않는다. 

대신에 클래스 변수는 클래스 내부의 메소드에서 모두 공유되는 변수이므로 중첩 함수에서 변경하건, 바깥 함수에서 변경하건 클래스 변수의 값이 모두 변경된다. 

class Solution(object):
    longest = 0

    def longestUnivaluePath(self, root):
        // code

2. 모든 경우에 대해서 DFS 탐색을 하고 경우에 따라 세분화

DFS 탐색은 leaf 노드에 도달할 때까지 계속 자식 노드를 호출하다가 leaf 노드가 발견되면 여기서부터 탐색을 시작한다. 그러므로 leaf 노드에 도달했을 때 실행할 base case를 만들어 주자.

leaf 노드 하나에 대해서만 DFS 탐색을 실행한다고 가정하면 당연히 가장 긴 경로값은 0이므로 0을 리턴한다. 

if node is None:
    return 0

모든 경우에 대해서 DFS 탐색을 한다. 이때 이진 트리라서 왼쪽, 오른쪽 두 방향으로 탐색이 가능하므로 왼쪽 자식 노드와 오른쪽 자식 노드 모두에 대해서 각각 탐색을 진행한다. 

left = dfs(node.left)
right = dfs(node.right)

이때 left와 right는 각각 왼쪽, 오른쪽 자식 노드까지 DFS 탐색을 했을 때 가장 긴 경로를 나타낸다. 

이는 DFS 중첩 함수의 리턴값으로, 클래스 변수에 저장되는 값과는 다르다. 

DFS 중첩 함수의 리턴값은 leaf 노드에서부터 올라가면서 탐색을 시작하고, 계속 같은 값을 가진 노드가 나올 때마다 1씩 증가한다. 중간에 다른 값인 노드가 나오면 다시 0으로 초기화된다. 

if node.left and node.val == node.left.val:
    left += 1
else:
    left = 0
    
if node.right and node.val == node.right.val:
    right += 1
else:
    right = 0
    
return max(left, right)

반면 클래스 변수에 저장되는 값은 DFS 중첩 함수에서 리턴되는 값과 자기 자신을 계속 비교해서 더 큰 값을 저장한다. DFS 탐색 중 중간에 다른 값인 노드를 만나서 리턴값이 0으로 초기화되더라도 클래스 변수의 값은 초기화되지 않는다는 차이가 있다. 

self.longest = max(self.longest, left + right)

* 해당 포스트는 <파이썬 알고리즘 인터뷰> 공부 후 정리 목적으로 작성되었습니다. *

leetcode 543번 ( https://leetcode.com/problems/diameter-of-binary-tree/ )

✅교재를 참고하지 않은 풀이: BFS

1차 시도(실패)

이진 트리의 직경(diameter)은 가장 거리가 먼 두 노드간의 거리이다. 

그래서 root 노드를 기준으로 왼쪽 subtree에서 가장 root에서 멀리 떨어진 노드와 오른쪽 subtree에서 가장 root와 멀리 떨어진 노드의 거리를 잰 뒤, 둘을 합하면 될 것이라고 생각하고 접근했다. 

그러나 예외가 있었다. 

위의 트리처럼 한쪽 subtree에만 많은 노드가 위치한 경우, root를 기준점으로 나눠서 계산한 직경(=7)보다 하나의 subtree 안의 다른 노드를 기준으로 계산한 직경(=8)이 더 컸다. 

class Solution(object):

    def diameterOfBinaryTree(self, root):

        if root is None or (root.left is None and root.right is None):
            return 0

        heightLeft = 0
        heightRight = 0

        queueLeft = collections.deque([root.left])
        queueRight = collections.deque([root.right])

        if root.left is not None:
            while queueLeft:
                heightLeft += 1
                for _ in range(len(queueLeft)):
                    current = queueLeft.popleft()
                    if current.left:
                        queueLeft.append(current.left)
                    if current.right:
                        queueLeft.append(current.right)

        if root.right is not None:
            while queueRight:
                heightRight += 1
                for _ in range(len(queueRight)):
                    current = queueRight.popleft()
                    if current.left:
                        queueRight.append(current.left)
                    if current.right:
                        queueRight.append(current.right)
        
        return heightLeft + heightRight

따라서 root 노드만을 기준으로 왼쪽, 오른쪽 subtree의 leaf 노드까지의 거리를 비교하면 안 되고 모든 노드를 기준으로 이 작업을 반복해서 가장 큰 값을 구하면 된다. 

✅교재를 참고한 풀이: DFS

BFS를 사용하지 않고 DFS를 사용하면 더 간단하게 풀 수 있었다. 

위의 경우 BFS는 맨 위의 root 노드부터 시작했지만 DFS는 leaf 노드에 도달하기 전까지는 탐색을 계속한다. 

DFS의 경우 재귀로 구현할 수 있고, 가장 긴 직경 값은 변수를 하나 선언하고 그 값을 업데이트 하면서 진행하면 된다. 그러나 가장 긴 직경 값은 숫자 변수인데, 숫자형은 변할 수 없기 때문에(immutable) 재귀함수 내부에 업데이트 로직을 작성해도 값이 바뀌지 않는다. 

그러므로 여기서는 직경 값 변수를 클래스 내부 변수로 선언했다. 이러면 self.longest 으로 해당 클래스 내부 변수에 접근할 수 있으므로 재귀 함수로도 같은 변수에 접근해서 값을 업데이트 할 수 있다. 

class Solution(object):
    longest = 0
    
    def diameterOfBinaryTree(self, root):
        //

이제 dfs()를 실행할 재귀함수 내부를 보자. 

재귀함수는 항상 반복적인 코드와 기본 상태(base case)가 필요하다. dfs()는 TreeNode 타입의 노드를 매개변수로 받고 dfs 탐색을 진행한 뒤 해당 노드의 레벨을 숫자로 리턴한다. 이 노드가 null 값일 경우 탐색을 하지 말아야 하므로 이 상태를 base case로 정하자. 

이때, null인 노드는 leaf 노드보다 더 하위 단계에 위치하므로 0이 아니라 -1을 리턴한다. 

if node is None:
    return -1

반복 로직의 경우, 한 노드를 기준으로 left subtree, right subtree 각각에 대해 dfs를 실행한다.

left = dfs(node.left)
right = dfs(node.right)

반복 로직이 실행되는 경우는 해당 노드가 left, right subtree를 가진 노드라고 볼 수 있다. 

(leaf 노드의 경우, null 값을 갖는 노드를 left, right subtree로 갖고 있다고 볼 수 있다.)

따라서 left, right subtree의 높이를 계산해서 더 큰 것을 선택한 다음에 1을 더해 준다. 해당 노드는 left, right subtree의 부모 노드이기 때문이다. 

return max(left, right) + 1

또한 가장 큰 직경 값도 업데이트 해 주어야 한다.

앞서 dfs()에서도 높이를 계산할 때 left, right subtree의 높이에다 1을 더했다.

한 노드를 중심으로 계산한 직경이 가장 크다는 의미는 직경을 계산하는 두 노드가 각각 해당 노드의 left subtree, right subtree에 위치한다는 말이다. 그러므로 두 subtree의 높이를 더한 뒤 1을 두 번 더해야 한다. 

self.longest = max(self.longest, left + right + 2)
return self.longest

* 해당 포스트는 <파이썬 알고리즘 인터뷰> 공부 후 정리 목적으로 작성되었습니다. *

leetcode 104번 ( https://leetcode.com/problems/maximum-depth-of-binary-tree/ )

✅교재를 참고하지 않은 풀이: 재귀

input으로는 TreeNode 타입의 root 노드 하나가 주어지고, 이를 통해 트리 전체의 깊이를 알아내는 문제이다. 

root 노드부터 아래로 내려가면서 트리 전체를 탐색해야 하므로 재귀 함수로 구현할 수 있다. 

탐색하는 노드의 값이 없거나, 탐색하는 노드의 left, right child 노드가 모두 없다면 탐색을 중단하고 현재까지 탐색한 깊이 값을 리턴한다.

탐색하는 노드의 값이 있다면 현재 깊이에 1을 더해준다. 

특정 노드의 높이는 현재 노드에서부터 leaf 노드에 도달하는 데 필요한 레벨(경로) 개수이다. 이때 left subtree와 right subtree의 leaf까지의 경로 수가 다를 수 있는데 이 경우 더 긴 쪽을 골라야 한다. 

class Solution(object):

    def maxDepth(self, root):

        if root is None:
            return 0
        
        def traverse(node, count):
            if node is None:
                return count

            if node.left is None and node.right is None:
                return count
            
            return max(traverse(node.left, count+1), traverse(node.right, count+1))

        return traverse(root, 1)

✅교재를 참고하지 않은 풀이: BFS

트리의 레벨을 탐색하는 경우 BFS로도 풀 수 있다. 

DFS는 스택으로 구현하며 LIFO 구조이고, BFS는 큐로 구현하므로 FIFO 구조이다. 

root 노드에서 시작해서 가장 위의 노드들부터 큐에 넣을 것이고, FIFO 구조이므로 그 노드들이 먼저 나올 것이다. 

참고로 파이썬에서 큐를 구현할 때는 데크(deque) 자료형을 사용하는 것이 일반적이다. 파이썬이 아닌 C언어로 구현된 모듈이기도 하고, 정확히는 큐가 아닌 데크이기 때문에 맨 앞과 맨 뒤에서 원소를 제거, 추가하는 것이 모두 가능하기 때문이다. 

맨 처음 root 노드를 큐에 넣은 상태가 시작 상태이다. 

deque = collections.deque([root])

BFS는 재귀함수로 구현할 수 없으므로 반복문을 사용한다. while문으로 큐가 빌 때까지 실행한다. 

먼저 큐의 맨 앞에서 원소를 하나 뺀다. 맨 처음은 root 노드가 될 것이다. 

그리고 이 노드의 left, right child가 있는지를 각각 확인하고 있다면 큐의 맨 뒤에 추가한다. 

current = queue.popleft()

if current.left:
    queue.append(current.left)
if current.right:
    queue.append(current.right)

주의할 점은 현재 큐에 있는 모든 노드를 대상으로 해당 노드들의 left, right child를 추가해야 한다. 그래야 큐에 레벨 순서대로 노드들이 들어올 수 있다. 

즉 while문이 한 번 실행될 때마다 이전 레벨의 노드를 큐의 앞쪽에서부터 전부 제거하고, 그 다음 레벨의 노드를 큐의 맨 뒤에 추가한다고 볼 수 있다. 현재 큐에 있는 모든 노드들에 대해서 위의 로직을 적용하려면, while문 내부에 별도의 for loop를 선언해서 큐의 길이만큼 반복해 주면 된다. 

* 해당 포스트는 <파이썬 알고리즘 인터뷰> 공부 후 정리 목적으로 작성되었습니다. *

leetcode 787번 ( https://leetcode.com/problems/cheapest-flights-within-k-stops/ )

DFS를 사용한 풀이(시도 but 실패)

class Solution(object):

    def findCheapestPrice(self, n, flights, src, dst, k):
        visited = set()
        graph = collections.defaultdict(list)
        for a, b, c in flights:
            graph[a].append([b, c])

        totalPrice = [2**31 -1]

        def dfs(node, price, times):
            if node in visited:
                return
            if node == dst:
                totalPrice[0] = min(totalPrice[0], price)
            if times > k:
                return
            else:
                times += 1
                while graph[node]:
                    entry = graph[node].pop(0)
                    dfs(entry[0], entry[1]+price, times)
                times -= 1
                visited.add(node)

        dfs(src, 0, 0)
        if (totalPrice is None) or totalPrice[0] == 2**31-1:
            return -1
        return totalPrice[0]

✅접근 방법

스택으로 DFS를 구현하고 다익스트라 알고리즘을 사용해서 풀 수 있다. 

다익스트라의 경우 이전 문제처럼 최소 힙을 구현한 heapq 모듈을 사용해서 풀 수 있다. 

다익스트라 알고리즘은 단순히 노드를 순회하면서 거리(dist) 값을 더 적은 것으로 업데이트하는 것이 아니라서 헷갈릴 수 있다. 탐색할 다음 노드를 정할 때 임의로 정하지 않고, 현재 노드에서 가장 거리가 적은 노드로 업데이트를 해야 한다. 

직접 구현하는 방법도 있지만 대부분 가장 거리가 적은 다음 노드를 불러올 때 최소 힙 등이 구현된 모듈을 사용하면 시간을 절약할 수 있다. 

✅구체적인 순서

1. 탐색 중인 노드에 대해서 출발점부터 현재 노드까지의 거리(price)와 탐색한 횟수(k) 정보를 저장하고 있는 변수를 만든다. 이때 key는 현재 노드, value는 리스트 형식으로 [현재 노드와 인접한 노드, 그 노드까지의 거리]를 나타낸다.  

graph = collections.defaultdict(list)
    for a, b, c in flights:
        graph[a].append([b, c])

2. heapq 모듈을 적용하기 위한 튜플-리스트 변수(여기서는 Q)를 선언한다. 이때 리스트 내부의 튜플은 (거리, 현재 노드, 탐색 횟수)를 정보로 갖고 있다. 거리를 제일 앞에 두는 이유는 heapq 모듈에 원소를 넣고 정렬할 때 튜플의 가장 앞 순서를 가장 우선으로 정렬하기 때문이다. 

times = 0
Q = [(0, src, times)]

그리고 스택으로 DFS 탐색을 할 경우 while문을 사용하며 스택 변수에 원소가 없어질 때까지 특정 로직을 반복한다. 

while Q:
    // 내부 로직

while문 내부 로직

3. min heap의 특성상 힙 내부에서 가장 거리가 작은 값만 리턴한다. 따라서 이 값들 중 dst(도착점)과 같은 노드가 있다면 탐색을 종료해도 무방하다. -> 해당 로직 만들기

price, node, times = heapq.heappop(Q)
if node == dst:
    return price

4. 또한 최소 힙에서 나온 탐색 횟수의 값이 제한된 탐색 횟수(k)보다 많다면 해당 노드에 대해선 DFS 탐색을 더 이상 실행하지 않는다. 

5. 위 조건을 만족할 경우 해당 노드의 주변 노드에 대해 탐색을 실행한다. 해당 노드의 주변 노드가 무엇인지 알기 위해서는 1번에서 선언한 변수를 사용한다. 

if times <= k:    
    times += 1
    for b, c in graph[node]:
        alternative = price + c
        heapq.heappush(Q, (alternative, b, times))

6. while문이 끝나도 도착점을 찾지 못했으면 -1을 리턴한다. 

✅불필요한 탐색 방지 로직

(다른 블로그를 참고했습니다.)

그런데 이대로 구현하면 input 개수가 많은 테스트케이스에 의해서 타임아웃이 뜬다. 로직은 맞지만 불필요한 탐색이 실행되고 있기 때문이다. (여러 노드가 얽힌 경우 순환 구조가 만들어지면서 이미 탐색한 노드를 또 탐색하게 된다.) 따라서 추가적인 로직이 필요하다. 

이미 탐색을 진행했고 노드의 값(price)이 최소 힙에서 나온 값보다 작다면, 이미 최소값에 대해서 탐색이 끝난 노드이므로 추가로 탐색할 필요가 없다. 구현하기 위해서는 어떤 노드를 탐색했고, 해당 노드의 값이 얼마인지를 저장하는 변수가 필요하므로 빈 딕셔너리 변수를 선언하자. 

visited = {}

if node not in visited or visited[node] < times:
    visited[node] = times

참고한 포스트

https://8iggy.tistory.com/115

* 해당 포스트는 <파이썬 알고리즘 인터뷰> 공부 후 정리 목적으로 작성되었습니다. *

leetcode 743번 ( https://leetcode.com/problems/network-delay-time/ )

시도

class Solution(object):

    def networkDelayTime(self, times, n, k):
        if n == 1:
            return 0

        queue = collections.deque()
        visited = set()
        graph = collections.defaultdict(list)
        for a, b, c in times:
            graph[a].append([b, c])

        dist = collections.defaultdict(lambda:float('inf'))
        dist[k] = 0
        count = 0
        queue.append(k)

        while queue:
            node = queue.popleft()
            for k, v in graph[node]:
                if k not in visited:
                    dist[k] = min(dist[k], dist[node]+v)
                    queue.append(k)
            visited.add(node)
        
        result = max(dist, key=lambda x:dist[x])
        return dist[result] if len(dist) == n  else -1

풀이. (교재 참고)

다익스트라(Dijkstra) 알고리즘을 구현하는 문제이다. 

다익스트라 알고리즘은 BFS 탐색으로 구현되며, DFS와 달리 재귀함수로 처리할 수 없다. BFS 탐색을 할 때에는 큐를 사용한다. 

노드 A에 대해서 BFS를 실행하는 경우, A의 주변 노드의 값을 모두 업데이트하고 그 주변 노드들을 큐에 추가한다.

이후 A를 큐에서 제거하는 방식으로 구현한다. 

다만 A를 제거하고 큐에서 다음 값을 불러올 때는 값이 가장 작은 노드 순서대로 불러와야 한다. 

이런 정렬을 매번 따로 할 수도 있겠으나 교재에서는 힙(heap)과 heappush(), heappop()을 사용해서 힙 내부에서 자동으로 정렬이 되도록 구현하였다. 

우선, 힙을 사용하기 전에 노드 A와 A에서 신호를 보낼 수 있는 노드, 신호를 보내는 데 걸리는 시간 정보를 더 효율적인 자료구조에 넣을 필요가 있다. 

딕셔너리를 사용해서 노드 A를 key값으로, 뒤의 두 값을 하나의 튜플로 묶어서 A를 key값으로 하는 리스트의 원소로 추가하자. 

graph = collections.defaultdict(list)

for u, v, w in times:
    graph[u].append((v, w))

출발 노드 k로부터 노드 A까지 신호가 도달하는 시간을 저장하는 변수도 필요하다. O(1) 만에 조회할 수 있는 딕셔너리 형식으로 선언한다. 

값을 변경할 때는 기존의 값과, 주변 노드의 시간을 참고해서 새로 계산된 값 중에서 더 작은 값으로만 변경될 수 있도록 해야 한다. 

여기서는 힙을 사용하기 때문에 힙 내부에서 이미 정렬이 되고, 시간이 오래 걸리는 경우 힙의 뒤 순서에 위치하게 된다. 또한 이미 탐색한 노드는 탐색하지 않는 방법으로 이런 오류가 발생할 가능성을 없앴다. 

또한 모든 노드를 탐색할 수 있는 경로가 없다면 -1을 리턴해야 한다. 모든 노드가 탐색되지 않은 경우 dist 딕셔너리의 길이가 n개 미만일 것이므로, dist 길이를 확인해서 -1을 리턴할지, 최댓값을 리턴할지를 판단하자. 

return max(dist.values()) if len(dist) == n else -1